2020年四月份的時候,住在紐約的大衛測試新冠病毒得到確診的結果,同期間另一個住在台北的大衛也得到確診的結果。兩個人都沒有出現症狀,但都被納入當地確診人口的統計數字。
但是我可以告訴你,即使在已經確診的情況下,紐約的大衛其實真的有被病毒感染的機率只有 93%,而台北的大衛真的有被感染的機率更低,只有 29%。
為什麼呢?第一,所有的測試本身都是有誤差的,比如說,真的有病卻未被偵測到,這叫做假陰性(false negative);而其實沒病卻被測出有病,這叫做假陽性(false positive)。關於測試的準確性,在醫學上或是統計學上,至少可以分為兩種:
(1)敏銳性(sensitivity)指的是在真的有病的人當中能夠正確測出陽性(true positive)的比例
(2)明確性(specificity)指的是在真的無病的人當中能夠正確測出陰性(true negative)的比例

任何一種統計的誤差若能壓低到5%,其結論就具有非常有效性。所以不管是敏銳性或明確性,若能達到95%,就算是很了不起了。目前以新冠病毒的測試來說,實驗室裡用RT-PCR的測式結果是最準確的,也最昂貴,但其敏銳性落差很大,從 70% 到97%不等;唾液測試是 72%,鼻腔抹拭63%,喉嚨抹拭則只有32%。
第二,大部份人在做類似的認知判斷時,常常犯一種忽略環境因素的基準比例的毛病,只用既得數字而草率地推論出比實際情況嚴重的結論。這是所謂的「忽略基準比例的謬誤」(base rate neglect fallacy),這無論在機率學或認知心理學的領域,都是很有名的一種常見的錯誤判斷行為模式。
所有測試結果的解讀牽涉的都是機率問題,而在做此機率判斷之前,必須先根據之前已得的數據來建立統計模型。這過程中,採樣及數據的讀取方法都會影響最後的判讀結果。因為我們的測試結果是把個人數據放進一個經過採樣的模型,在做解讀時必須將這一步納進考量,才能獲得真正更準確的機率做為結論。
以新冠病毒為例,先讓我們假設其測試非常精準,誤診(false positive) 的機率只有 5%。所以當大衛(不管是紐約的大衛還是台北的大衛),被確診之後,一般人會認為這就表示 95% 的機率他的確是被感染了。但我卻告訴你,他真正被感染的機率其實低於 95%。
讓我們先以紐約為例。假設紐約這個疫區的感染率是 40%,也就是說,每1000個人當中有400個人會被感染,這一步的數字來自之前經過採樣而得到的模型。如果我們假設測試非常嚴格,其敏銳性高達100%(也就是說真的有病的人都不會被漏掉),但有5 %的 false positive rate (也就是每100個無病的人當中有五個人會被誤診為有病)。我們可以用以下的表格及簡單的數字來表示:
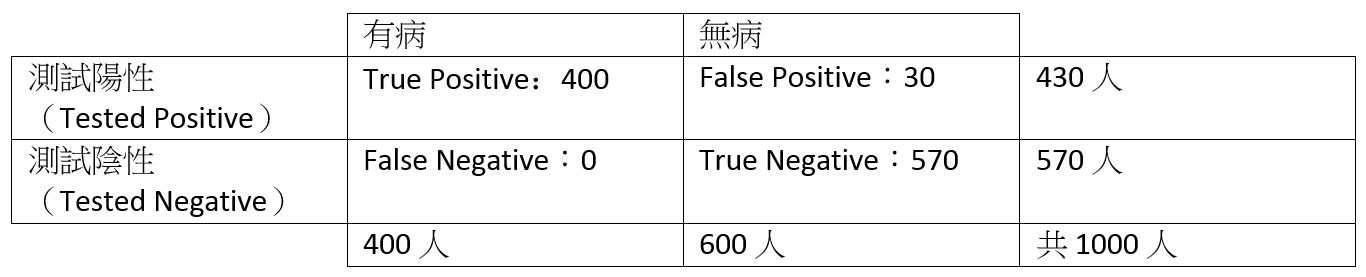
對於被確診的紐約大衛來說,現在已知的是他是430人當中的一個。此時當我們要再更進一步來瞭解他真正被感染的機率,看他是否屬於真正有病的那400人之一。 也就是說,在已得知確診的情況底下,他真正有感染的機率是:400 /430 = 93%。
那麼同樣被確診,對於台北大的衛為什麼會有不一樣的解讀呢?原因是台北的感染率很低,也就是環境不同,所套用的模型不同,基準比例(base rate)不同。同樣的表格,若我們把感染率改為 2%,
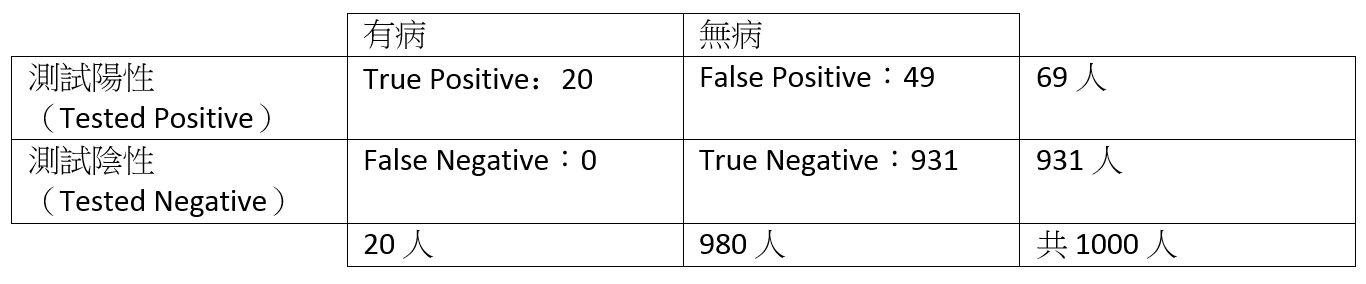
對於被確診的台北大衛來說,現在已知的是他是69人當中的一個。此時當我們要再更進一步來瞭解他真正被感染的機率,看他是否屬於真正有病的那20人之一。也就是說,在已得知確診的情況底下,他真正有感染的機率是:20 /69 = 29%。
比較以上兩個例子,我們可以發現,在不同的狀況或地區,因為套用的模型(基準比例)不同,即使測試結果一樣,但在做機率判斷時卻會有不同的解讀。紐約的 40%及台北的 2%,就是所謂的「基準比例」。一般人卻會直接忽略這個部份,單單只看最後的測式結果。
在這個例子我們還假設敏銳性為100%,而這在真實生活裡是不可能的。隨著敏銳性的降低,真正有染病的機率還會再更低。以下是以台北為例,當測試敏銳性只有80%的時候,即使被測出陽性,台北大衛真正染病的機率只有 24.6%。
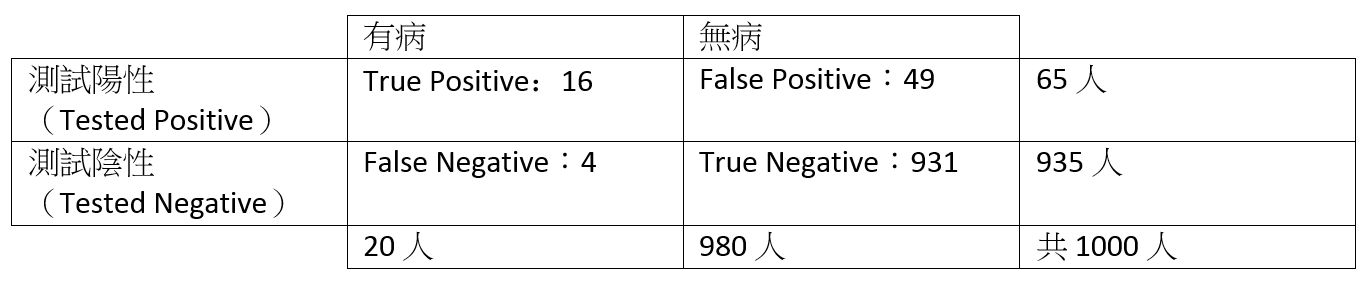
以上的機率解讀的例子所套用的感染率(基準比例)是假設在全部人口裡隨機採樣,但如果今天會去接受測試的人不是隨機的,而是有經過特殊挑選(例如已經有症狀的),那麼因著採樣範本的不同,基準比例就會不同,所以最後判讀也將會有所不同。
正因為統計本身有許多可調整的參數,差之毫釐,失之千里。因此若如果沒有搞清楚數字的來源及採樣的方法,隨便拿一個報告數字來當作真理,就很容易自己嚇自己。這是人們日常生活裡常犯的一種謬誤。